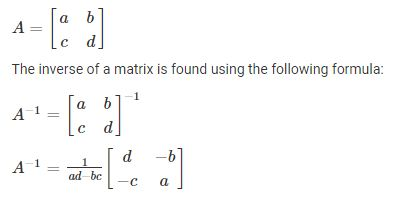Matrices and Vectors

Vectors, matrices, basic facts

• A vector x ∈ $\mathbb{R}^{n}$ is a column vector. The corresponding row vector is $x^T$.

• $\mathbb{R}^{m \times n}$ is the set of real matrices with m rows and n columns. $\mathbb{C}^{m \times n}$ is the set of complex $m \times n$ matrices.

  This is a m by n matrix:

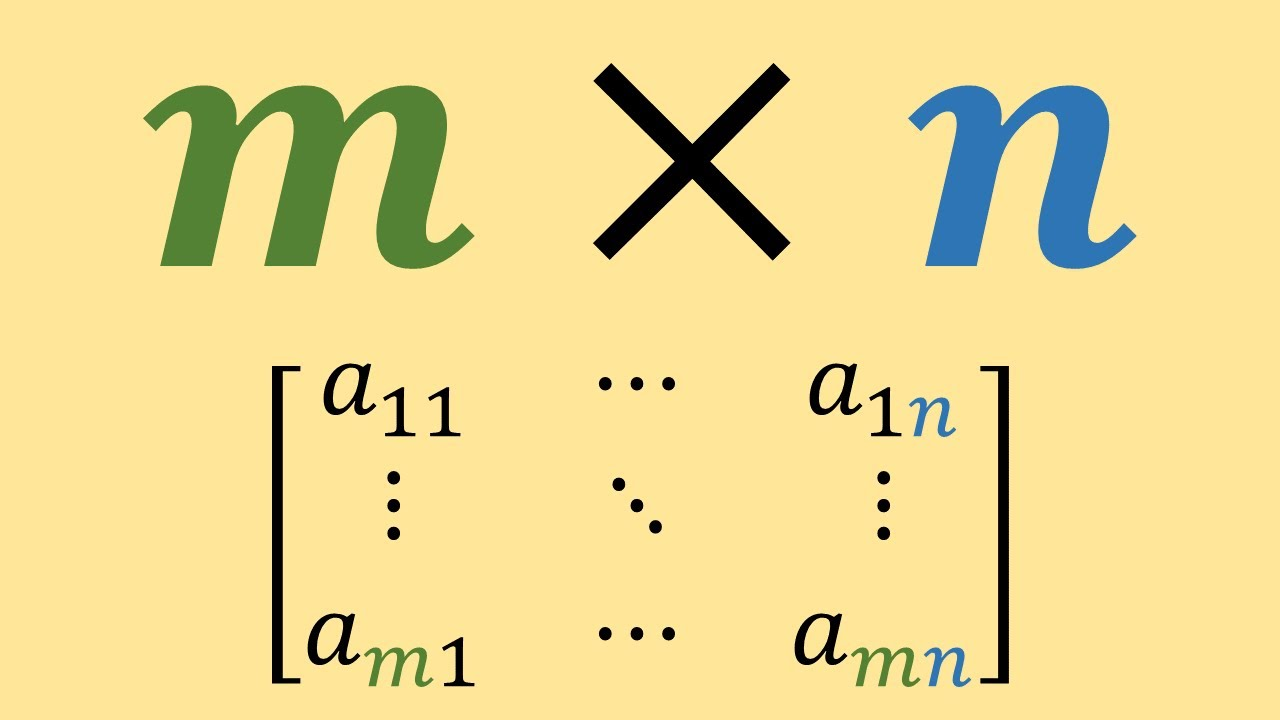
• Notation: $A$ denotes the matrix, $a_{ij}$ is an element of the matrix $A$, i.e. $a_{ij}$ = $(A)_{ij}$ . Use upper case for matrices and lower case for vectors.

  

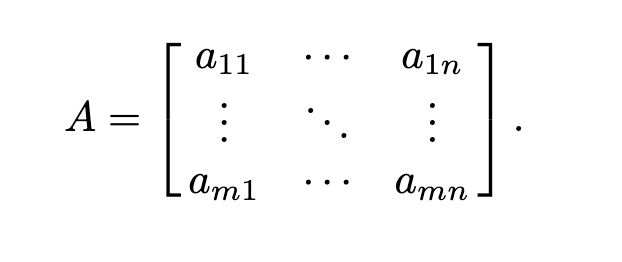
Block matrices: A matrix can be represented in block form, for example

where $A \in \mathbb{R}^{n \times n}, B \in \mathbb{R}^{n \times m}, C \in \mathbb{R}^{m \times n}, D \in \mathbb{R}^{m \times m}$. The dimensions of the blocks must be compatible.

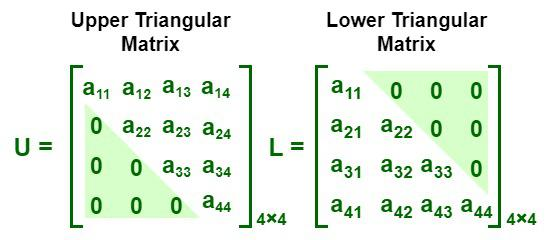
Upper/Lower Block Triangular Matrix and Upper Triangular Matrix

The matrix

is upper block triangular. Note that it is not upper triangular (it has elements below its main diagonal).

Transpose: $A^T \in \mathbb{R}^{n \times m}$ is the transpose of $A \in \mathbb{R}^{m \times n}$. $(A^T)_{ij} = a_{ji}$.

Hermitian transpose (also called conjugate transpose): $A^H \in \mathbb{C}^{n \times m}$ is the hermitian transpose of $A \in \mathbb{C}^{m \times n}.$ Example of Hermitian transpose:

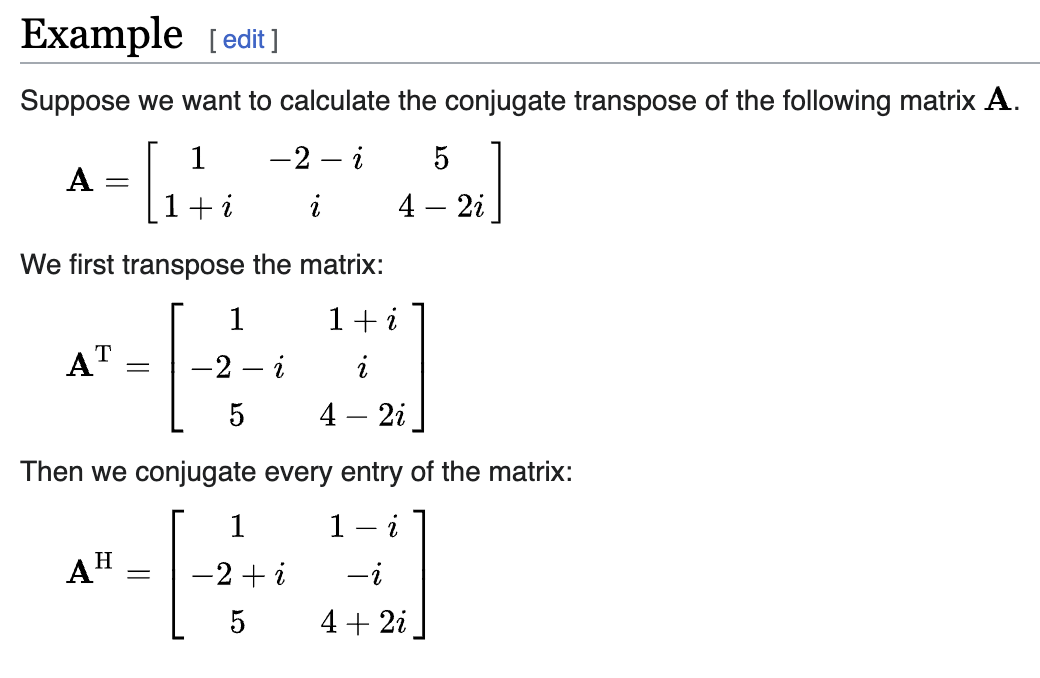
• Definition:

  The conjugate transpose of an $m \times n$ matrix A is formally defined by:

  $(A^H)_{ij} = \overline{A_{ji}}$

  where the subscript $ij$ denotes the $(i,j)$-th entry, for $1 \leq i \leq n$ and $1 \leq j \leq m$, and the overbar denotes a scalar complex conjugate.

  The definition can also be written as:

  $A^H = (\overline{A})^T$$= \overline{(A^T)}$

  Some notations:

  

• Steps for Hermitian transpose:
  1. Transpose $m \times n$ matrix $A$ to $A^T$
  2. Applying complex conjugate on each entry (the complex conjugate of $a + ib$ being $a - ib$, for real number $a$ and $b$.

Note (Overline notation):

In complex number, the overline notation can indicate a complex conjugate and analogous operations.

• if $x = a + ib$, then $\overline{x} = a - ib$

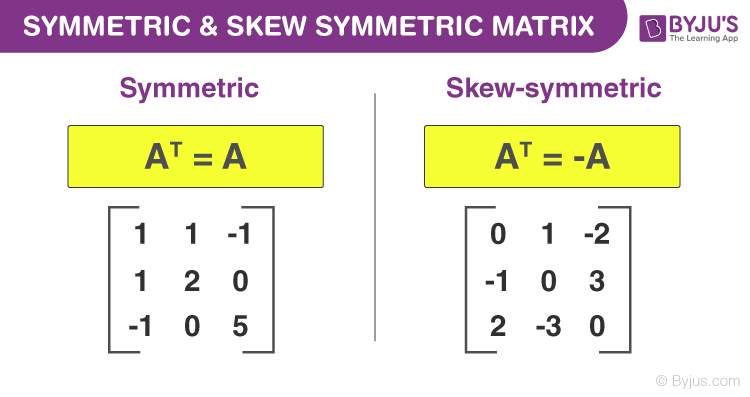
Symmetric matrix:

$A = A^T$

Skew-symmetric matrix:

$A^T = -A$, $a_{ji} = -a_{ij}$

Hermitian matrix: $A = A^H$

Matrix multiplication: $A \in \mathbb{R}^{m \times n}, B \in \mathbb{R}^{n \times p}, C \in \mathbb{R}^{m \times p}, C = AB. \space c_{ij} = \sum_{k=1}^{n} a_{ik}b_{kj}.$ Note that in general $AB \neq BA$.

• Example:

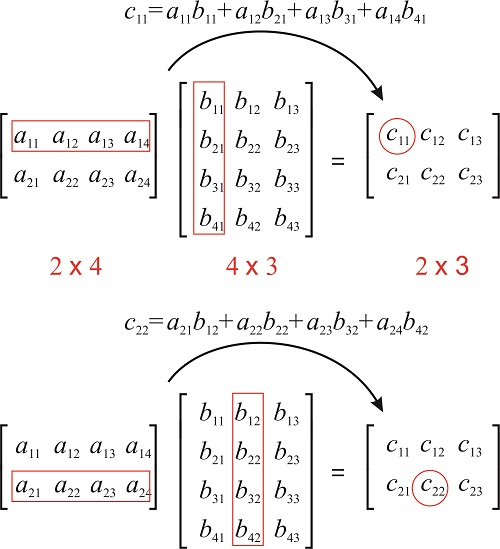
• Transpose:

  $(AB)^T = B^TA^T$

• Note:

  If $A \in \mathbb{R}^{a \times b}, B \in \mathbb{R}^{c \times d}$, then $b = c$, $AB \in \mathbb{R}^{a \times d}$

Dot Product of Vectors:

$x,y \in \mathbb{R}^{n}$, the dot product of $x$ and $y$ is $x^Ty = \sum_{i=1}^{n} x_iy_j$

Example:

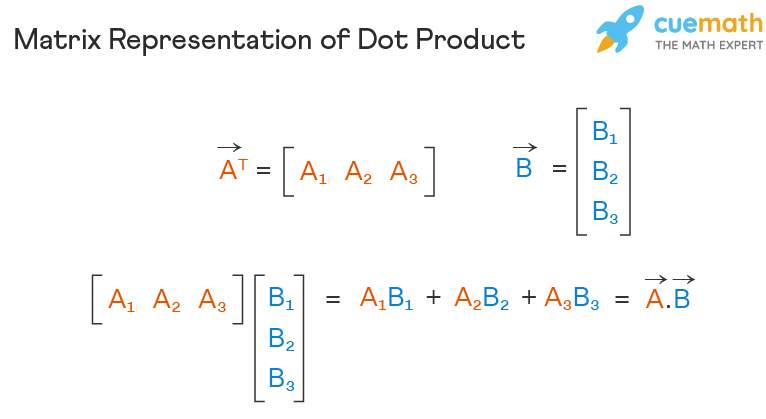
Outer product of vectors: $x, y \in \mathbb{R}^n$, the outer product of x and y is an $n \times n$ matrix of rank one. $A = xy^T$. $a_{ij} = x_iy_j$.

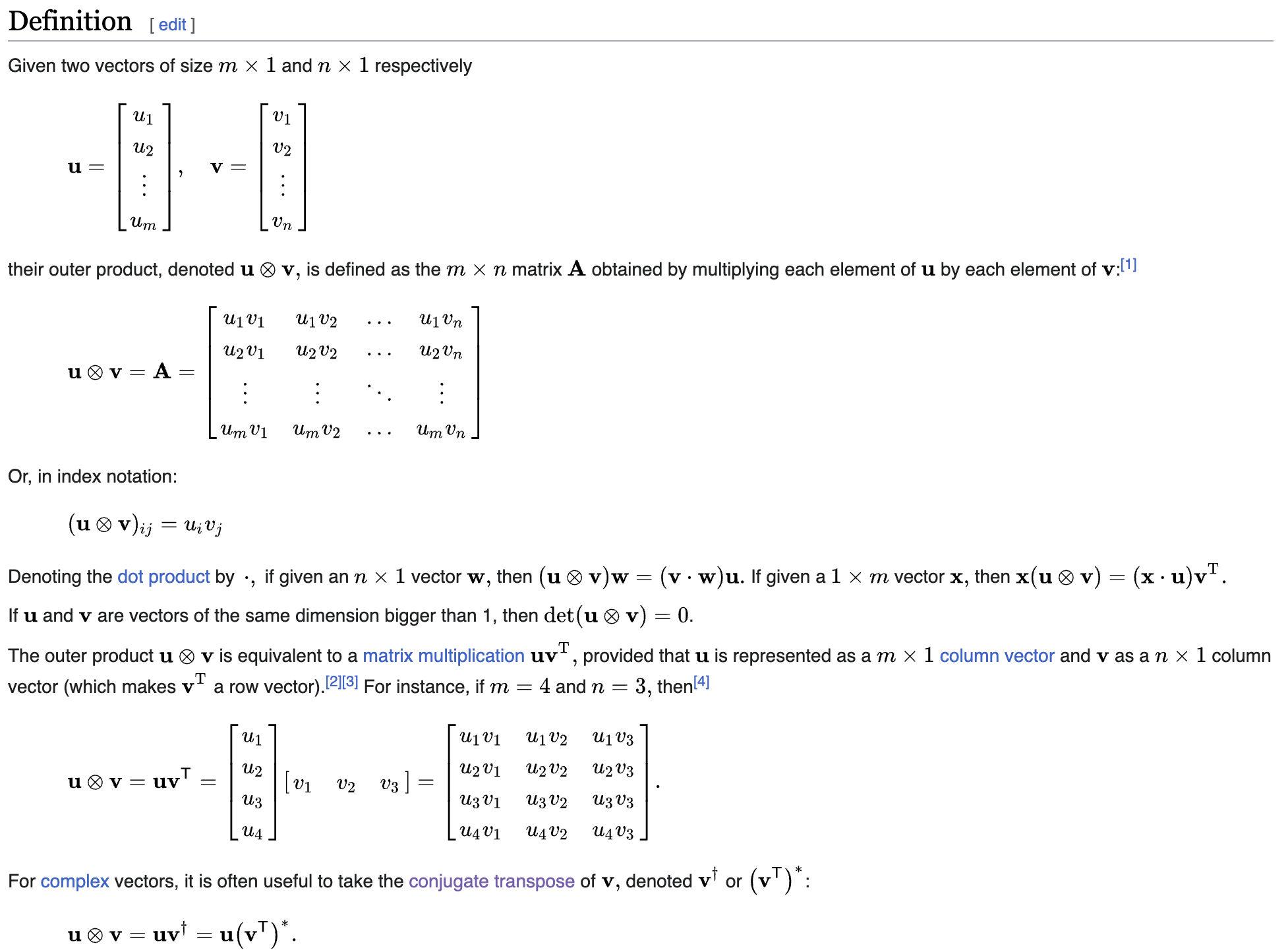
Transpose of a product: $(AB)^T = B^TA^T$

Complex dot product: $x^Hy = \sum_{i=1}^{n} \overline{x_i}y_i$. This is not symmetric: $x^Hy = \overline{y^Hx}.$

Orthogonal matrix: $A\in\mathbb{R}^{n \times n}, A^TA=AA^T = I$.

Example:

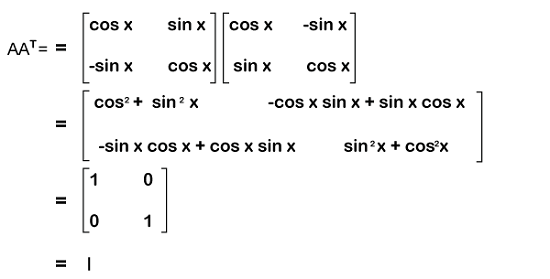
Unitary matrix: $A\in\mathbb{C}^{n \times n}$, $A^HA = AA^H=I$.

Example:

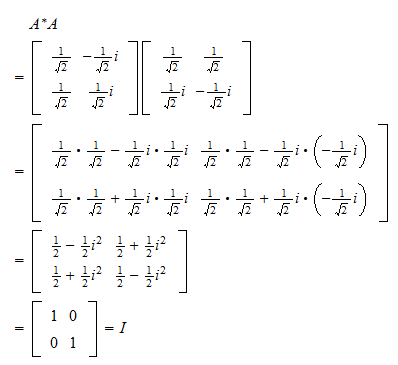
Matrix algebra, basic facts

• In general, for matrices $A,B,C$, if $AB$ $=AC$ for $A \neq 0$, this does not imply that $B=C$. If $AB=0$, this does not imply that either $A$ or $B$ is zero.

• Matrix inverse: $A \in \mathbb{R}^{n \times n}$, the inverse of $A$ is $A^{-1}$ such that $AA^{-1}=A^{-1}A$$=I$.

  

• Trace: $TrA = \sum_{i}a_{ii}. \space Tr(A+B)= TrA+TrB. \space Tr(AB)= Tr(BA)$. $\space Tr(cA) = cTr(A)$. $Tr(A)=Tr(A^T)$.

  Definition: The trace of an $n \times n$ square matrix $A$ is defined as

  

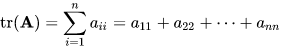
  where $a_{ii}$ denotes the entry on the $i$th row and $i$th column of $A$. The entries of $A$ can be real numbers, complex numbers, or more generally elements of a field F. The trace is not defined for non-square matrices.

  Example:

Proof Tr(AB) = Tr(BA):

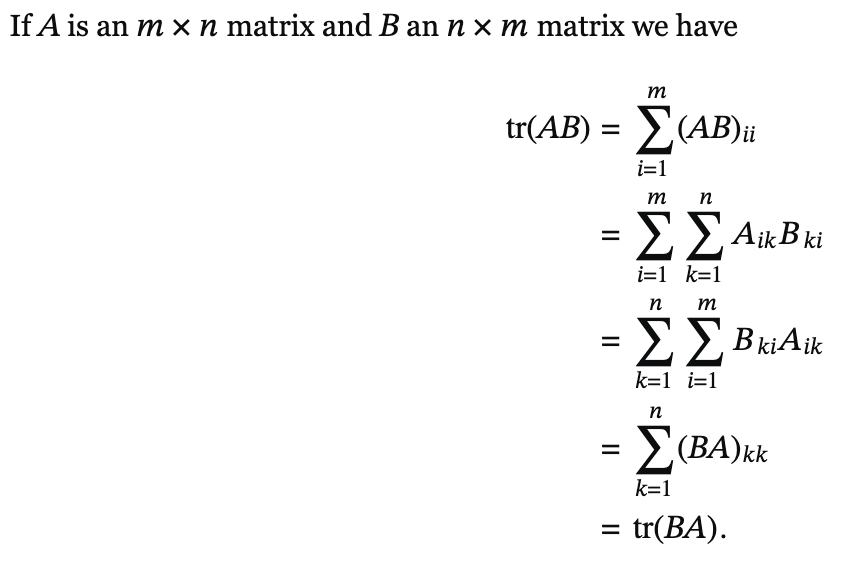
• Determinant: $A\in \mathbb{R}^{n \times n}$

  

  $$det A^T = det A, \space detA^H = \overline{detA}, \space detAB= detAdetB,\space det \alpha A = \alpha^n detA$$

  

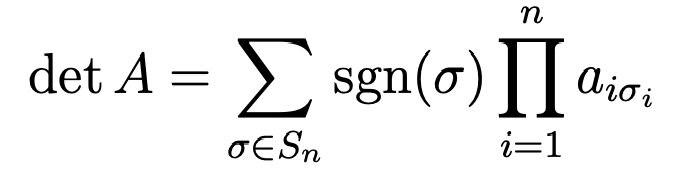
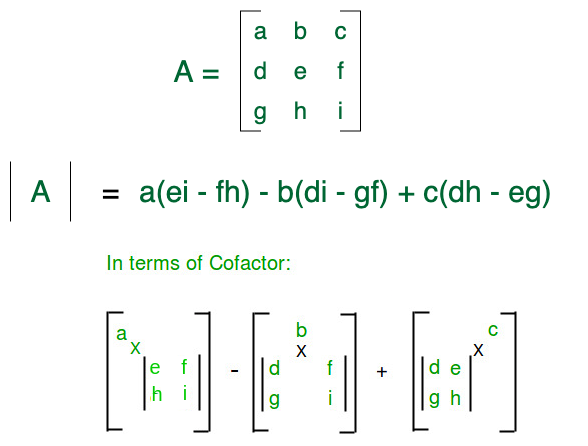
  Why Determinant: The determinant of a matrix is a single numerical value which is used when calculating the inverse or when solving systems of linear equations. The determinant of a matrix A is denoted |A| , or sometimes det(A)

• Schur Complement: (Upper graph: if $A$ an invertible matrix, then $D-CA^{-1}B$ is the Schur complement of $A$; lower graph: if $D$ an invertible matrix, then $A-BD^{-1}C$ is the Schur complement of $D$)